Mathematical models can complement experimental and clinical studies but also challenge current paradigms redefine our understanding of mechanisms driving tumorigenesis and. Mayo Clinic and Mayo Foundation RochesterUSA 2.

Mathematical modeling is a description of a system or a process through mathematical language.
Mathematical modeling of tumor growth. Using mathematical models to simulate dynamic biological processes has a long history. Over the past couple of decades or so quantitative approaches have also made their way into cancer research. An increasing number of mathematical physical computational and engineering techniques have been applied to various aspects of tumor growth with the.
Mathematical modeling of tumor growth and tumor-host interactions and summarize some of the seminal and most prominent approaches. Ordinary differential equation partial differential. Mathematical modeling of tumor growth.
The MCF-7 breast cancer cell line. Breast cancer is the second most commonly diagnosed cancer in women worldwide. MCF-7 cell line is an extensively studied human breast cancer cell line.
This cell line expresses estrogen receptors and the growth of MCF-7 cells is hormone dependent. Mathematical modeling is a useful tool to elucidate new mechanisms involved in tumor growth kinetics which can be relevant to understand cancer genesis and select the most suitable treatment. Mathematical Modeling of Tumor Growth Kinetics 1.
Mayo Clinic and Mayo Foundation RochesterUSA 2. University of Zagreb ZagrebCroatia. Mathematical modeling has been developed in oncology in order both to understand and predict tumor growth and to anticipate the effects of targeted or non-targeted therapies eg.
There is a very wide range of these models involving many stages in tumor progression. Mathematical modeling has been critical for the description of tumor growth which is a highly complex process as a finely chiseled tumor growth model always outlines the measurements and the physiological processes of the tumors. Therefore a mathematical model involving partial differential equations for the growth of tumor have been studied modified and developed in this paper.
In this work we developed a mathematical model that incorporated the dynamics of four coupled cell populations including tumor cells natural killer cells dendritic cells and cytotoxic T cells that influence the growth of tumors. The novelty in the model was how it combined important interactions between growing tumor cells and cells of the innate and specific immune system coupled with models for. Comparison of mathematical tumor growth models Johanna Sápi Dániel András Drexler Levente Kovács Research and Innovation Center of Óbuda University Physiological Controls Group Óbuda University Budapest Hungary Email.
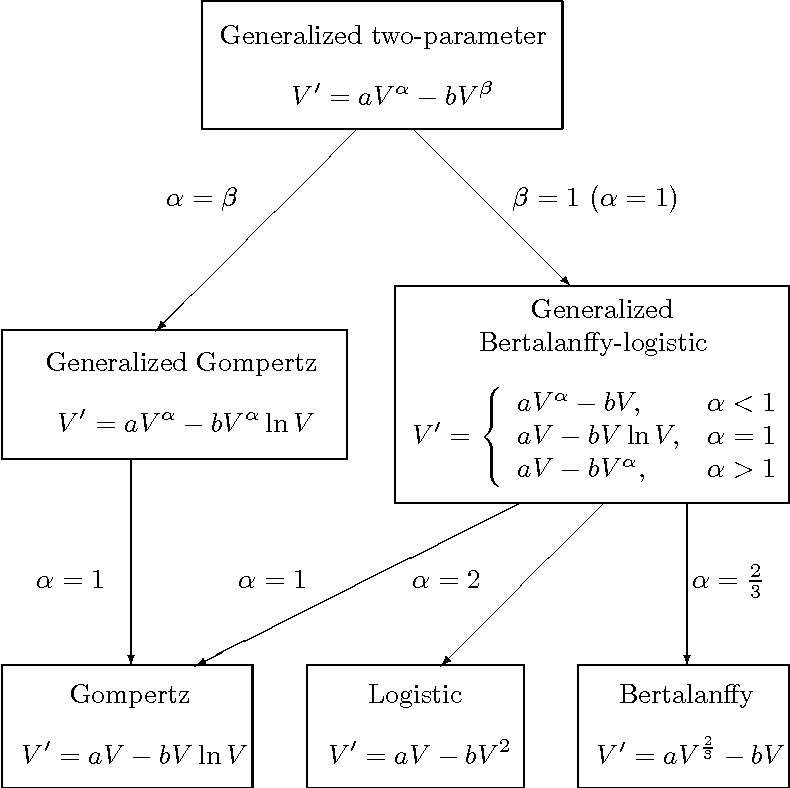
Seven ordinary differential equation ODE models of tumor growth exponential Mendelsohn logistic linear surface Gompertz and Bertalanffy have been proposed but there is no clear guidance on how to choose the most appropriate model for a particular cancer. Mathematical modeling of tumor growth helps us better understand such patterns and analyze drug efficacy in transplanted tumor models. Many mathematical models have been proposed to describe tumor growth curves each with certain assumptions and equations suitable for specific situations or data sets1-5.
Breast tumor growth is then studied using the mathematical model. The results obtained from numerical simulation are compared with those from clinical and experimental studies. The system has three coexisting stable equilibria representing the tumor free state a microscopic tumor and a large tumor.
Some simple mathematical models of tumor growth This equation takes into account that resources are limited and this fact tends to slow the growth of cells. Verhulst introduces the logistic model which says that the populations growth rate is not constant but rather depends on the size of the. The objective of this work is to use mathematical modeling to understand the mechanisms that regulate tumor growth and metabolism.
A hallmark of cancer is cell-intrinsic metabolic reprogramming that enhances anabolic support of cell proliferation and leads to metabolic heterogeneity in tumors at larger scales. Quantitative models addresses many questions regarding tumour initiation progression and metastases as well as intra-tumour heterogeneity treatment responses and resistance. Mathematical models can complement experimental and clinical studies but also challenge current paradigms redefine our understanding of mechanisms driving tumorigenesis and.
Mathematical modeling and simulation play an increasing prominent role in cancer research serving as a tool for theoretical analysis and prediction of clinical trials. Simply put cancer is uncontrolled tumor growth plus angiogenesis the growth of new blood vessels. We developed a simple mathematical model of tumor growth and its response to radiation by incorporating two key characteristics.
I the tumor growth rate decreases as the tumor volume increases and ii some radiation-damaged cells still keep dividing for a few more cell cycles after a single pulse of irradiation. Mathematical Models of Avascular Tumor Growth. This review will outline a number of illustrative mathematical models describing the growth of avascular tumors.
The aim of the review is to provide a relatively comprehensive list of existing models in this area and discuss several representative models in greater detail. Mathematical modeling is a description of a system or a process through mathematical language. In modeling prostate tumor growth we encounter obstacles at two levels.