Box 49 H-1525 Budapest Hungary bResearch Institute for Solid State Physics and Optics PO. Evolutionary games on graphs.
Basedonequations1214and15thetransitionprobabilitiesare givenby p00 ii1 μ i ia n ic μ i n i n 25 p0 ii n ic ia n ic μ i 26 p ii1 ν i ib n id ν i i n 27.
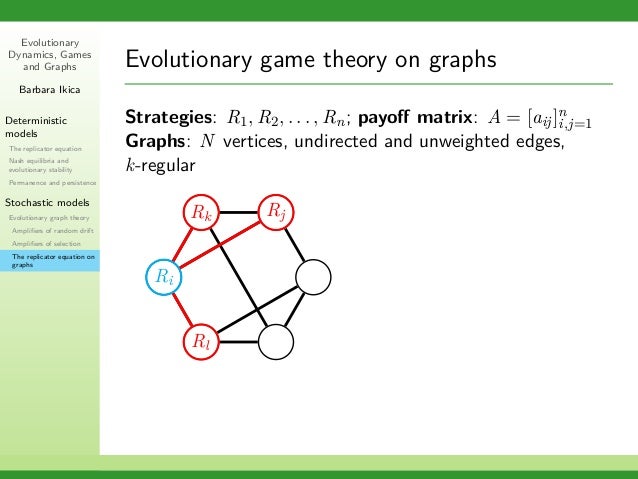
Evolutionary games on graphs. Evolutionary games on graphs 1. Game theory is the unifying paradigm behind many scientific disciplines. It is a set of analytical.
The goal of 2 Rational game theory 3 Evolutionary games. Population dynamics 4 Evolutionary. Evolutionary games on graphs.
The first four sections introduce the necessary background in classical and evolutionary game theory from the basic definitions to the most important results. The fifth section surveys the topological complications implied by non-mean-field-type social network structures in general. The next three sections.
Recently I study evolutionary games on lattices and graphs by considering systematically the effects of orthogonal matrix components describing games with self- and cross-dependent payoffs. Evolutionary games on graphs. We focus primarily on exact results for graphs with symmetry complementing earlier reviews 95 82 87 that take a wider view of the field.
Our review is organized as follows. In Section 2 we present the basic model for evolutionary games on graphs and review a variety of update rules compatible with this model. These effects can be modeled using evolutionary games on graphs.
Recently conditions were derived for a trait to be favored under weak selection on any weighted graph in terms of coalescence times of random walks. Here we consider isothermal graphs which have the same total edge weight at each node. The conditions for success on isothermal graphs take a simple form in which the effects of.
The fourth section surveys the topological complications implied by non-mean-field-type social network structures in general. The last three sections discuss in detail the dynamic behavior of three prominent classes of models. The Prisoners Dilemma the Rock-Scissors-Paper game and Competing Associations.
The major theme of the review is in what sense and how the graph structure. Evolutionary games on graphs. Download Full PDF Package.
A short summary of this paper. 37 Full PDFs related to this paper. Evolutionary games on graphs.
Evolutionary games on graphs. Evolutionary games on graphs György Szabóa Gábor Fáthb aResearch Institute for Technical Physics and Materials Science PO. Box 49 H-1525 Budapest Hungary bResearch Institute for Solid State Physics and Optics PO.
Box 49 H-1525 Budapest Hungary Accepted 18 April 2007 Available online 29 April 2007 editor. Evolutionary two-player games on graphs with edge diversity. In each generation an individual plays a two-player game with each neighbor to derive a payoff and accumulates its payoffs from all interactions.
We endow each type of edges with an independent payoff matrix. Let us now turn to evolutionary games on graphs 18 19. Consider as before two types A and B but instead of having constant fitness their relative fitness depends on.
Abstract Game theory is one of the key paradigms behind many scientific disciplines from biology to behavioral sciences to economics. In its evolutionary form and especially when the interacting agents are linked in a specific social network the underlying solution concepts and methods are very similar to those applied in non-equilibrium statistical physics. This review gives a tutorial-type.
This observation is in line with previous results for pairwise games on graphs suggesting that the condition for the evolution of cooperation is optimized when interaction and replacement neighborhoods coincide which corresponds to our assumption of individuals playing a single game. Future work should consider the calculation of structure coefficients for the cases where the payoff to. Mathematical studies of evolutionary games on graphs16171820212223242526272829have typically assumed that the graph is regular meaning that each individual has the same number of.
Game theory is one of the key paradigms behind many scientific disciplines from biology to behavioral sciences to economics. In its evolutionary form and especially when the interacting agents are linked in a specific social network the underlying solution concepts and methods are very similar to those applied in non-equilibrium statistical physics. This review gives a tutorial-type overview.
Abstract In this paper we investigate evolutionary games with the invasion process updating rules on three simple non-directed graphs. The star the circle and the complete graph. Here we present an analytical approach and derive the exact solutions of.
We use pair approximation to describe the evolutionary game dynamics on regular graphs of degree k. In the limit of weak selection we can derive a differential equation which describes how the average frequency of each. Evolutionary games on graphs 1331 a bc Figure1aAstargraphwithN 6verticesandn 5leavesbacirclewithN 6vertices andcacompletegraphwithN 6vertices.
Basedonequations1214and15thetransitionprobabilitiesare givenby p00 ii1 μ i ia n ic μ i n i n 25 p0 ii n ic ia n ic μ i 26 p ii1 ν i ib n id ν i i n 27. Evolutionary dynamics are affected by population structure mutation rates and update rules. Spatial or network structure facilitates the clustering of strategies which represents a mechanism for the evolution of cooperation.
Mutation dilutes this effect. Here we analyze how mutation influences evolutionary clustering on graphs. In this paper we investigate evolutionary games with the invasion process updating rules on three simple non-directed graphs.
The star the circle and the complete graph. Here we present an analytic approach and derive the exact solutions of the stochastic evolutionary game dynamics.
